1.Вводная
информация о постоянных магнитах
Издревле,
магниты считались
вещью загадочной. Древние греки называли магнитный железняк
- камнем Гекулеса. Да и сейчас обсуждается много идей
разного рода вечных двигателей и т.п. Но мы в данной заметке
постараемся рассмотреть сугубо утилитарную сторону применения
постоянных магнитов.
Постоянный магнит оказал огромное влияние на историю человечества. В
первую очередь это
касается магнитного компаса , остающегося и поныне надежным средством
морской
и воздушной навигации. Во-вторых, постоянный магнит стал одним из
главных
факторов, повлиявших на исследования электродинамических
процессов
и приведших в итоге к созданию электродинамики как науки, и всей
многообразной электродинамической техники.
Однако, до последнего времени практическое применение постоянных
магнитов в области техники ограничивалось в основном следующими
отдельными, хотя и весьма важными, применениями:
- телефон
и
динамический громкоговоритель
- микроэлектродвигатель
- системы возбуждения небольших электрогенераторов
- поляризованные реле
- измерительные, научные и медицинские приборы-
- маломощные держатели ( магнитные защелки, ловители, сепараторы
и т.п.)
Эти устройства характеризуются,
как правило, небольшими мощностями, усилиями и моментами. Везде, где
нужно
было увеличивать силу или мощность устройства, конструкторская мысль
обращалась к использованию электромагнитов (соленоидов),
распространившихся в технике куда более широко, но имеющих и свои
ограничения и особенности.
Однако, за
последние 30 лет свойства постоянных магнитов революционным образом
изменились, что хорошо видно из приведенной ниже диаграммы.
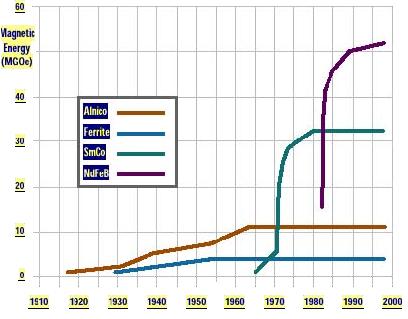
Нижняя
голубая линия показывает динамику развития свойств ферритовых магнитов,
именно тех, которые мы используем обычно в защелках, динамиках и т.п.
Следующая красная - магнитные сплавы типа Альнико
( алюминиево-никелиевые),
применяемые обычно в радио и телевизионной аппаратуре.
А вот зеленая и фиолетовая - соответствуют новому виду магнитов,
изготавливаемых на
основе редкоземельных элементов:
- зеленая линия - Самарий-
кобальтовые магниты,
- фиолетовая
линия - Неодим -
железо - боровые.
Как видно из диаграммы магнитная энергия самариевых магнитов в 6 раз
выше, а неодимовых в 10 раз выше , чем у привычных нам ферритовых (
керамических) изделий. На практике это
означает, что неодимовый магнитик, размером c куриное
яйцо, неосторожно взятый в руки, - способен раздробить пальцы. Т.е.
механические усилия , которые могут создаваться современными
постоянными магнитами уже не являются силами игрушечными или
приборными, а вполне соответствуют усилиям, характерным для обычных
машин и механизмов, т.е - десятки и сотни килограммов.
Такие свойства делают возможным,
например, изготовление различных малогабаритных механических и
электромеханических удерживающих устройств с высоким усилием фиксации,
например станочных приспособлений, грузоподьемных устройств и т.п.
Естественно, что опыта использования мощных магнитов в нашей
обычной мебельной технологии пока нет, исключая магнитные
сепараторы для древесной стружки на плитных
заводах. Эти знания остаются пока достоянием
специалистов - электромехаников.
Поэтому представляется,
что конструктор, механик или технолог любого предприятия, в том
числе и мебельного или деревообрабатывающего, должны знать больше
о редкоземельных магнитах, как об одном из важных и перспективных
направлений развития современной техники и технологии.
По закону Ампера ( в простой скалярной форме F = I х L х B) , на
проводник с током, помещенный в магнитное поле действует сила F,
пропорциональная длине проводника L, силе тока I и величине магнитной
индукции B. Поэтому, электромеханические
устройства ( электрические двигатели, реле и т.п. приводные и др.
элементы техники ) основанные на явлении электромагнитной индукции
и в которых применены магниты нового типа при сохранении своих
размеров становятся значительно сильнее. Т.е. пропорционально
увеличению величины магнитной индукции возрастает крутящий момент или
тяговое
усилие или скорость движения ( врашения). Или же, при сохранении
мощности устройства соответственно уменьшаются его габариты и
вес. В некоторых случаях, применение новых магнитов
позволяет существенно снизить расход электроэнергии, и это не
противоречит законам физики.
Примечание
. Цена машины,
станка или др. устройства, в том числе и шкафа,
прямо связана с его материалоемкостью. Во многих случаях эта
зависимость
- едва ли не прямая пропорция, что, впрочем, когда нибудь станет
понятным
и мебельщикам.
Более подробно и с картинками
можно посмотреть закон Ампера и др. основные понятия электромагнетизма
в любом школьном учебнике или справочнике по физике.
Прозводство
магнитов на основе редкоземельных элементов давно миновало лабораторную
стадию и в последние несколько лет развивается быстрыми темпами
по достаточно гибким технологиям, в том числе и в нашей стране, и они
доступны
любому заказчику. Хотя магниты называются редкоземельными, но
фактически,
природные ресурсы ( руды и рудные концентраты ) в нашей странеи
для
их производства весьма велики.
По данным ООО "Химсталькомплект"
постоянные магниты NdFeB, из известных в настоящее время
систем, занимают уникальное положение по соотношению
характеристики/стоимость, что объясняет бурный рост их производства и
внедрение в различные отрасли. Так, в 1989г. было произведено 190, в
1999г. 13500, а 2000г.-17500 тонн металлокерамических магнитов и
магнитопластов. По прогнозам аналитиков к 2005г. будет произведено
около 40000 тонн магнитов NdFeB. "
Некоторые примеры конструкций
производимых отечественных магнитов показаны в таблице:
| Сегменты различной
геометрии и
направленности поля: |

радиальной намагниченности |
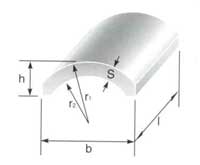
h, b, l,s, R1, R2 — геометрические параметры сегмента |
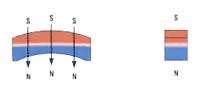
параллельной намагниченности |
| Призмы |
 |
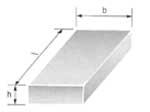
h, b, l — геометрические параметры призмы |
| Кольца — с различным
количеством
полюсов и направлением поля |
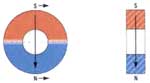
2-х полюсное кольцо |

4-х полюсное кольцо |

|
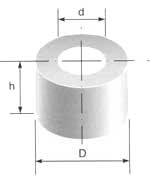
|
| Цилиндры |
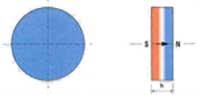
|
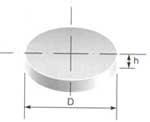
|
| Магниты
сложных форм |
 |
Современные
технологии позволяют изготавливать магниты и других сложных
геометрических форм.
Эти рисунки и следующая ниже таблица
характеристик магнитных материалов
взяты со страницы ООО "Химсталькомплект" http://www.metalopt.ru
2. Свойства современных постоянных магнитов
Основные
характеристики
магнитных материалов
| Материал
|
(BH)
max,
МГс*Э |
B r
, Гс |
H c
, Э |
Цена, $
за 1 кг на
российском рынке |
Цена, $
на единицу
(BH)max |
| Гибкие
магнитные материалы |
1.6 |
1725 |
1325 |
5-10 |
3.1- 6.2 |
Керамика
( феррит) |
3 |
4000 |
2400 |
1-2.5 |
0.3-0.85 |
| Альнико |
9 |
13500 |
1400 |
44.1 |
4.3 |
| Sm-Co |
20 |
10500 |
9200 |
250 -500 |
12.5 |
| Спеченные
Nd-Fe-B |
50 |
14200 |
12500 |
70-150 |
1.4-3.7 |
Br - остаточная индукция, т.е.
основная
силовая характеристика постоянного магнита , BHmax - энергетическое
произведение
3. Формулы для расчета постоянных магнитов
Ниже приведены
методы и
формулы для приблизительного расчета несложных магнитных систем на
основе постоянных магнитов, рекомендуемые английской фирмой Dexter, вполне
доступные для понимания пожилого дровосека. Все
последующие формулы, комментарии и картинки взяты непосредственно со
страницы фирмы , правда не
могу поручиться за абсолютную точность моего перевода.
Расчет магнитной индукции
аксиально-намагниченных цилиндрических магнитов с радиусом (r)
и длиной (l ), в точке расположенной на расстоянии (d)
от повехности, вдоль оси производится по формуле:
Пример:
r=0.5", l=1", d=0.25",
B r
=12200 Gauss, B=2935.7 Gauss
Расчет методом граничных элементов ( МГЭ), B=2788.7
Gauss
Расчет магнитной индукции для
призматических
магнитов намагниченных по длине , толщиной (2t), шириной (2w
) и длиной ( l), для точки
расположенной на расстоянии (d) от поверхности вдоль магнитной
оси производится по формуле:
Пример:
2t=1", 2w=1", l=0.5", d=0.25",
Br=12200, B=2386.5
Gauss
Используя МГЭ, B=2238 Gauss
Расчет магнитной индукции в точке
вдоль осей
этих геометрий более комплексный. Есть три компонента магнитной
индукции, которые должны быть приняты во внимание . но принцип остается
тем же. Подобные формулы приемлемы для прямоугольных магнитов.
Цилиндрические магниты труднее поодаются расчету, для них рекомендуются
компьютерные методы расчета.
При использовании принципа совмещения,
могут
быть подвергнуты анализу магниты и более сложных геометрических форм.
Для примера , мы можем рассчитать магнитную индукцию вдоль оси
цилиндрической трубы по формуле:
Вычитая магнитную индукцию
внутреннего
цилиндра с диаметром (2 ri ) из магнитной
индукции цилиндра с внешним диаметром (2r0
), мы получаем магнитную индукцию трубы ( которая обычно используется в
Фарадеевых поворотных устройствах).
Подобная логика может быть приложима
и к другим
магнитам симметричной формы:
Используя принцип суперпозиции ,
можно
определить магнитную индукцию в промежутке между двумя соосно
расположенными магнитами:
Индукция между двумя
призмами
на расстоянии (d) определяется по формуле B = B
1 + B
2 , где B 2 -
индукция от призмы на расстоянии (g-d).
Приближенно, результаты таких
расчетов могут
быть применимы к магнитам, размещенным в ненасыщенной стальной цепи.
Когда используются подобные формулы, обычно исходят из предположения ,
что
распределение индукции в стали соответствует индукции магнита двойной
длины. Если большая часть магнитного потока проходит через зазор ( т.е.
без потерь
в стали), то результат расчета имеет хорошую точность.
Для двух магнитов размещенных на
C-образной
скобе расчет производится по формуле:
B= B1 + B
2 , где B1 -
индукция прямоугольного блока дляной (2l) на расстоянии
( d). B 2 - индукция
прямоугольного блока длиной (2l ) на расстоянии ( g-d).
Пример: l=1", 2w=1",
2t=1", B r=12200 Gauss, g
=1", d=0.3", B 1=3033 Gauss, B2
B 1
+ B 2 =4243 Gauss,
используя МГЭ, B =4121 Gauss
=1210 Gauss,
Дальнейшие вариации на эту тему
бесконечны. Для
большей точности рекомендуются компьютерные расчеты
Расчет магнитных цепей
Эмпирический подход пригоден для
анализа цепи со
стальным сердечником или другими проницаемыми материалами. Начиная с
идеальной цепи не имеющей потерь и сопротивления в стали, этот метод
используется для эмпирического определения отношений в точных моделях
магнитных цепей.
Рисунок идеальной цепи см. ниже
Используя закон Ампера для цепи,
допускаем , что
в стали отсутствуют потери магнитодвижущей силы:
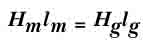
где Hm=MMF
магнита, lm =длина магнита, Hg
= MMF поперек
зазора, lg = длина
зазора.
Допуская , что весь поток
индукции проходит полностью через зазор ( т.е. без потерь) мы можем
написать следующее соотношение:
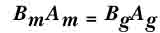
Где
Bm - индукция магнита, Am
- поперечное сечение магнита, Bg - поток через зазор
, Ag - поперечное сечение зазора.
Если мы допустим B m и Hm
и возьмем их соотношение , то мы
получим коэффициент
проницаемости (PC).
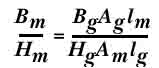
Проницаемость материала
определяется как µ=B/H. В системе CGS
проницаемость воздуха равна единице, таким образом Bg=Hg
. Тогда соотношение для коэффициента
проницаемости :
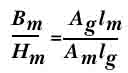
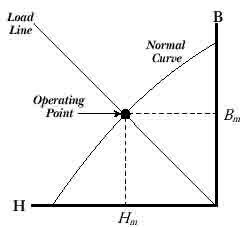
Коэффициент
проницаемости определяется на наклонной линии к началу координат.
Пересечение наклонной линии и второго квадранта кривой размагничивания
называется операционной точкой , где B и Hm
геометрически определены. От Bm, мы можем
расчитать индукцию в зазоре , ( Bg):
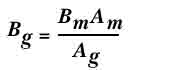
|
 |
Этот подсчет является
приблизительным , потому что не учитывает потерь индукции или MMF в
цепи. Фактор потерь (ó) и фактор сопротивления (f
) определяются эмпирически в соответствии с упомянутыми выше
отношениями ( для большей точности) .
Фактор потерь есть соотношение
общего магнитного потока к потоку в зазоре. Он определяется
проницаемостью, и аналогичен проводимости электрической цепи. A
magnetic circuit can usually be broken up into basic leakage paths. Для
каждой потерянной магнитной линии эмпирически определяется формула для
магнитной проводимости , которая может быть использована. Обычно
используются формулы из книги ( "Electromagnetic Devices " (
Электромагнитные устройства) написанной Herbert C. Roters (New York:
John Wiley
& Sons, Inc., 1941).
Фактор потерь определяется по фомуле :
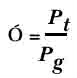
Где P t -
сумма проницаемости всех потерянных магнитных линий ( включая зазор)
цепи, Pg - проницаемость зазора.
Фактор сопротивления (f)
считается для потерь MMF в несущих магнитный поток
элементах цепи ( т.е. стали) и небольших зазорах между деталями. Этот
фактор определяется эмпирически и находится в пределах от 1,1 до 1.5
для большинства цепей. Большие значения относятся к цепям близким к
уровню насыщению стали. Фактор сопротивления:
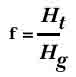
Где Ht
- суммарная MMF и H g - MMF
поперек зазора
Расчет магнитных сил
Обычно
импользуется
следующая формула для расчета удерживающей силы магнита :
F=0.577B2A
где B
- индукция в килогауссах, A - площадь полюса в
квадратных дюймах. Для магнитов, конструкция которых показана ниже
используется следующая формула:
F=0.577(B12A1+B2
2A2)
|
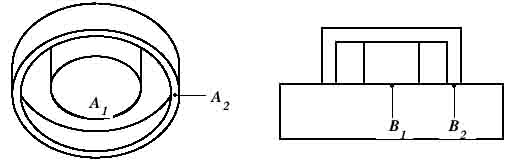 |
Для простых
магнитов отделенных от стальной пластины воздушным проиежутком (d),
с хорошей точностью для B может быть расчитано через
текущие соотношения.
Для магнита
непосредственно соприкасающегося со сталью , могут быть использованы
следующие два метода.
Если магнит имеет форму подобную диску или пластинке ( малое отношение
длина/диаметр) , используется следующая формула:
где Br=
остаточная индукция, lm = длина магнита и A=площадь
полюса.
Для магнитов
имеющих кубическую или призматическую форму или для тех, у которых
соотношение длины к диаметру равно 1 или более, результат может быть
получен с хорошей точностью. Допуская, что
индукция в стали
приблизительно эквивалентна индукции магнита двойной длины, мы можем
вычислить магнитную индукцию в центре используя следующее уравнение:
| Calculate B@d=-l |
F=0.577B2A |
Примечание . Облегчить эти расчеты
можно
используя, например, стандартные способы
из программы " Excel" пакета "Windows" или несколько специальных
магнитных калькуляторов, расположенных на сайте фирмы "Dexter " >>>
Для самостоятельного анализа и расчета
магнитных систем можно
рекомендовать так же очень интересный отечественный комплекс программ
для инженерного моделирования электромагнитных, тепловых и механических
задач методом конечных элементов ELCUT™ . Дружественный
пользовательский интерфейс, простота описания даже самых сложных
моделей, широкие аналитические возможности комплекса и высокая степень
автоматизации всех операций позволяют разработчику полностью
сосредоточиться на своей задаче не отвлекаясь на изучение
математических основ вычислительных алгоритмов и особенностей их
реализации. Ознакомиться с возможностями комплекса, пройти обучение и
получить бесплатно демоверсию программы можно непосредственно на
сервере ELCUT Для
начала освоения программы требуется всего несколько часов.
Достоинством программы является то, что выдаваемая цветная
графика очень удобна для понимания существа, т.е физики процесса.
По вопросам производства и применения современных постоянных магнитов в
сети имеется значительное количество источников на русском и
иностранном языках.
| |

